Trong cuộc sống hàng ngày, khái niệm vô hạn xuất hiện khắp nơi – từ những con số kéo dài vô tận trong toán học đến ý tưởng về vũ trụ không biên giới trong vật lý, hay thậm chí là sự vĩnh cửu trong triết học và tôn giáo. Tuy nhiên, vô hạn thường khiến chúng ta cảm thấy khó chịu về mặt logic: Nó chưa bao giờ được quan sát trực tiếp trong thực tế, nhưng lại không thể thiếu trong việc mô tả thế giới. Ví dụ, bộ số tự nhiên có thể tăng dần mãi mãi mà không có điểm dừng, nhưng liệu ai đó có thực sự đếm đến “vô hạn” không? Điều này đặt ra câu hỏi cốt lõi: Vô hạn có thực sự tồn tại, hay chỉ là một khái niệm trừu tượng để diễn tả những gì vượt quá khả năng nhận thức của con người? Từ góc nhìn cá nhân, tôi luôn thấy vô hạn như một “con quái vật” toán học – hấp dẫn nhưng đầy mâu thuẫn, thúc đẩy sự tò mò về bản chất của thực tại. Trong bài viết này, tôi sẽ khám phá lịch sử, các nghịch lý nổi bật, và ứng dụng của vô hạn qua lăng kính học thuật, kết hợp phân tích từ nội dung gốc (với các chỉnh sửa về lỗi chính tả, thông tin không chính xác như tên riêng và logic lộn xộn) cùng nguồn dữ liệu bổ sung từ các tài liệu uy tín, nhằm làm rõ khái niệm này một cách dễ hiểu nhưng sâu sắc.
Lịch sử khái niệm vô hạn: từ cổ đại đến hiện đại
Khái niệm vô hạn đã xuất hiện từ rất sớm trong lịch sử nhân loại, không chỉ như một ý tưởng toán học mà còn gắn liền với triết học và tôn giáo. Vào khoảng thế kỷ thứ 6 TCN, nhà triết học Hy Lạp Anaximander đã đề xuất “apeiron” – một nguyên lý vô hạn, vô định hình làm nền tảng cho vũ trụ, coi nó như nguồn gốc của mọi sự tồn tại. Trong văn hóa Ấn Độ cổ đại, ý tưởng về vô hạn liên quan đến vũ trụ và thần linh đã xuất hiện từ khoảng 1500 TCN, thường gắn với các khái niệm như chu kỳ vĩnh cửu trong Veda. Tuy nhiên, những mốc thời gian này chỉ phản ánh phần nổi của lịch sử, vì thiếu bằng chứng xác thực để xác định chính xác nguồn gốc.

Đến thế kỷ 5 TCN, Zeno of Elea – học trò của Parmenides – đã sử dụng vô hạn để tạo ra các nghịch lý nổi tiếng, nhằm bảo vệ quan điểm rằng chuyển động chỉ là ảo giác. Sau Zeno khoảng 100 năm, Aristotle phân biệt vô hạn thành hai loại: vô hạn tiềm năng (potential infinity) – như dãy số tự nhiên có thể kéo dài mãi mà không đạt đến điểm cuối – và vô hạn hiện thực (actual infinity) – một tập hợp hoàn chỉnh với vô hạn phần tử tồn tại đồng thời. Aristotle bác bỏ vô hạn hiện thực trong thế giới vật chất, cho rằng nó dẫn đến mâu thuẫn logic.
Sang thế kỷ 19, nhà toán học Georg Cantor đã cách mạng hóa khái niệm này qua lý thuyết tập hợp, chứng minh rằng có nhiều cấp độ vô hạn khác nhau – ví dụ, tập hợp số tự nhiên (đếm được, ℵ₀) nhỏ hơn tập hợp số thực (không đếm được, 2^ℵ₀). Cantor gặp phải sự phản đối mạnh mẽ từ các nhà toán học truyền thống, nhưng công trình của ông đã đặt nền móng cho toán học hiện đại. Từ góc nhìn cá nhân, lịch sử này cho thấy vô hạn không phải là “kẻ thù” của logic, mà là công cụ để mở rộng hiểu biết – dù đôi khi nó khiến tôi tự hỏi liệu con người có đang “chơi” với những khái niệm vượt quá giới hạn nhận thức của mình không.
Nghịch lý của Zeno: chuyển động có phải là ảo giác?
Zeno đã minh họa vô hạn qua các nghịch lý, như nghịch lý Achilles và con rùa: Achilles không thể đuổi kịp con rùa nếu phải liên tục vượt qua nửa khoảng cách còn lại, vì quá trình chia đôi kéo dài vô hạn. Tương tự, nghịch lý mũi tên: Tại bất kỳ khoảnh khắc nào, mũi tên đang bay dường như đứng yên, nên chuyển động chỉ là sự ghép nối của vô hạn khoảnh khắc tĩnh. Những nghịch lý này thách thức nhận thức thông thường về chuyển động và thời gian, gợi ý rằng thực tại có thể là ảo giác.
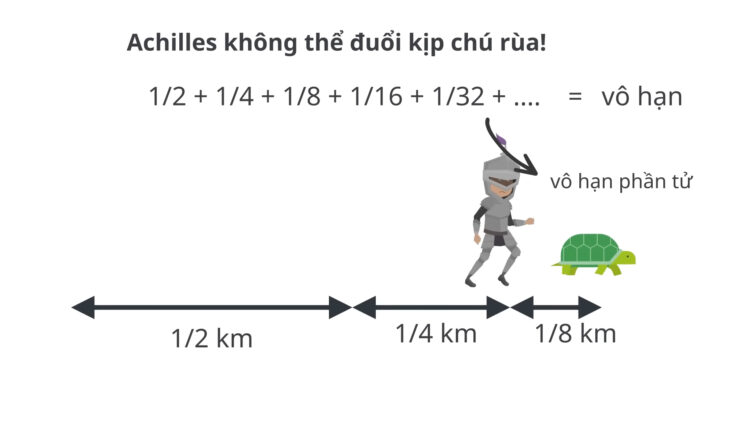
Giải quyết hiện đại đến từ toán học vi tích phân của Newton và Leibniz, mô tả chuyển động như dòng chảy liên tục qua tổng của vô hạn cấp số hội tụ. Trong vật lý lượng tử, thang đo Planck (khoảng 1.6 × 10^{-35} mét cho chiều dài, 5.4 × 10^{-44} giây cho thời gian) được coi là giới hạn nhỏ nhất, nơi không gian-thời gian có thể không còn liên tục, từ đó “dừng” quá trình chia đôi vô hạn của Zeno. Tôi nghĩ rằng, dù Planck scale chưa được chứng minh là giới hạn tuyệt đối, nó mang lại sự an ủi: Vô hạn toán học có thể không áp dụng trực tiếp vào thực tế vật lý, giúp chúng ta tránh bế tắc logic.
Vô hạn tiềm năng và hiện thực: từ Aristotle đến Cantor
Aristotle coi vô hạn tiềm năng như một quá trình không ngừng (như đếm số tự nhiên), trong khi vô hạn hiện thực là một thực thể hoàn chỉnh – điều ông cho là bất khả thi trong thế giới hữu hạn. Cantor đã chứng minh vô hạn hiện thực tồn tại toán học, qua định lý rằng tập hợp số thực lớn hơn tập hợp số tự nhiên.

Một ví dụ minh họa là nghịch lý khách sạn Hilbert: Một khách sạn với vô hạn phòng, dù đầy khách, vẫn có thể đón thêm vô hạn khách bằng cách dịch chuyển mỗi khách sang phòng tiếp theo (phòng 1 sang 2, 2 sang 3, v.v.). Điều này cho thấy vô hạn có thể “mở rộng” mà không cần thêm không gian, một ý tưởng nghe vô lý nhưng logic toán học. Từ trải nghiệm cá nhân, nghịch lý này khiến tôi suy nghĩ về dữ liệu kỹ thuật số: Bộ nhớ máy tính hữu hạn, nhưng chúng ta thường xử lý dữ liệu như thể vô hạn qua nén và thuật toán.
Vô hạn trong vật lý: từ hố đen đến lượng tử
Trong vật lý, vô hạn xuất hiện ở các điểm kỳ dị như trung tâm hố đen hoặc Big Bang, nơi mật độ và độ cong không gian-thời gian trở nên vô hạn theo thuyết tương đối tổng quát. Tuy nhiên, lý thuyết lượng tử coi vô hạn như dấu hiệu của mô hình chưa hoàn chỉnh, và sử dụng renormalization để loại bỏ chúng trong lý thuyết trường lượng tử – một quá trình “bỏ qua” vô hạn bằng cách điều chỉnh tham số để phù hợp thực nghiệm.
Các lý thuyết như lý thuyết dây và hấp dẫn lượng tử vòng cố gắng loại bỏ vô hạn bằng cách giả định không gian-thời gian rời rạc ở thang Planck. Tôi cảm thấy thú vị khi vô hạn ở đây đại diện cho “bế tắc” khoa học – không phải kết thúc, mà là lời mời khám phá sâu hơn, giống như Einstein từng nói về cấu trúc toán học ẩn giấu của vũ trụ.
Vô hạn trong triết học và tôn giáo: siêu hình và mâu thuẫn
Trong triết học, vô hạn thách thức lý trí, như Spinoza coi Thượng Đế là vô hạn và vô hạn. Trong tôn giáo, Hinduism xem vũ trụ như chu kỳ vô hạn (samsara), Buddhism nhấn mạnh vô hạn trong sự giác ngộ và vô thường, trong khi Islam mô tả Allah như vô hạn và vĩnh cửu. Những quan điểm này thường thuộc “trật tự tưởng tượng” (theo Yuval Noah Harari trong Sapiens), nơi vô hạn là niềm tin hơn là thực nghiệm.
Mâu thuẫn là cốt lõi: Chúng ta sống trong thế giới hữu hạn nhưng tư duy chấp nhận vô hạn, như chạy đua vũ trang để duy trì hòa bình – logic mâu thuẫn nhưng thực tế. Từ góc nhìn cá nhân, mâu thuẫn này không phải lỗi, mà là đặc tính nền tảng của ý thức, có lẽ liên quan đến tính song trùng sóng-hạt trong lượng tử.
Vô hạn là quy luật hay ảo giác?
Sau tất cả, vô hạn vẫn là khái niệm trừu tượng hoạt động theo quy luật, gắn liền với thời gian – nhưng toán học tồn tại độc lập với thời gian, làm công cụ giải mã vũ trụ. Tuy nhiên, nếu vô hạn chỉ tồn tại trong toán học, việc sử dụng nó để mô tả vũ trụ có thể tạo rào cản. Các nhà vật lý đang nỗ lực loại bỏ vô hạn, và tôi hy vọng lý thuyết như hấp dẫn lượng tử sẽ thành công. Cuối cùng, vô hạn nhắc nhở rằng não bộ chúng ta chưa đạt giới hạn, nhưng chính chúng ta đôi khi là rào cản. Bạn nghĩ sao – vô hạn là thực tại hay chỉ là công cụ tư duy? Hãy suy ngẫm, vì hành trình khám phá này dường như… vô hạn.




