Toán học ban đầu được phát triển như một cách định lượng thế giới của chúng ta—để đo đạc đất đai, dự đoán chuyển động của các hành tinh và theo dõi thương mại. Sau đó, xuất hiện một vấn đề mà người ta cho là không thể giải quyết được. Bí quyết để giải quyết vấn đề đó là tách rời toán học khỏi thế giới thực, chia tách đại số với hình học, và phát minh ra những con số mới đến mức được gọi là “số ảo.” Thật mỉa mai, 400 năm sau, chính những con số đó lại xuất hiện ở trung tâm của lý thuyết vật lý tốt nhất về vũ trụ. Chỉ khi từ bỏ mối liên hệ trực tiếp của toán học với thực tại, chúng ta mới có thể khám phá ra bản chất thật sự của hiện thực.

Năm 1494, Luca Pacioli – người từng là thầy dạy toán của Leonardo da Vinci – đã xuất bản cuốn Summa de Arithmetica, một bản tổng hợp toàn diện về toàn bộ kiến thức toán học đã biết ở Ý thời Phục hưng. Trong cuốn sách này có một phần nói về các phương trình bậc ba, tức là bất kỳ phương trình nào mà ngày nay chúng ta viết dưới dạng:
a·x³ + b·x² + c·x + d = 0
Suốt ít nhất 4.000 năm, con người đã cố gắng tìm ra nghiệm tổng quát cho phương trình bậc ba. Mỗi nền văn minh cổ đại từng gặp phải vấn đề này—người Babylon, Hy Lạp, Trung Quốc, Ấn Độ, Ai Cập và Ba Tư—đều không tìm được giải pháp. Pacioli kết luận rằng nghiệm của phương trình bậc ba là không thể tìm ra.
Điều này ít nhất cũng đáng để ngạc nhiên, vì nếu bỏ qua hạng x³, phương trình chỉ còn là phương trình bậc hai—và nhiều nền văn minh cổ đại đã giải được phương trình bậc hai từ hàng ngàn năm trước. Ngày nay, bất cứ ai đã qua lớp tám đều biết công thức chung của phương trình bậc hai:
x = (–b ± √(b² – 4ac))/(2a).
Tuy nhiên, hầu hết mọi người chỉ đơn giản là thế chỗ các số vào công thức này mà không nhận ra hình học ẩn sau mà các nhà toán học cổ xưa đã sử dụng để dẫn ra nó.
Vào thời đó, toán học không được viết thành các công thức ký hiệu như ngày nay mà được diễn đạt qua lời nói và hình vẽ. Ví dụ, hãy xét phương trình
x² + 26x = 27.
Các nhà toán học cổ đại thường hiểu hạng x² như là một hình vuông có cạnh dài x. Hạng 26x được hiểu như là một hình chữ nhật với một cạnh dài 26 và cạnh còn lại dài x, và tổng diện tích của hai hình này bằng 27. Để tìm giá trị của x, họ sẽ lấy hình chữ nhật 26x chia đôi thành hai hình chữ nhật 13x, sau đó sắp xếp chúng lại thành một hình vuông gần như hoàn chỉnh, chỉ thiếu đi một mảnh vuông có kích thước 13×13. Bằng cách “hoàn thiện hình vuông” (thêm một hình vuông 13×13), họ duy trì được tính đẳng thức bằng cách phải cộng thêm 169 (vì 13² = 169) vào bên còn lại của phương trình. Hình vuông mới có cạnh bằng (x + 13) và diện tích bằng 196, mà căn bậc hai của 196 là 14. Do đó, x + 13 = 14, suy ra x = 1. Phương pháp trực quan này là một cách hiệu quả để giải phương trình bậc hai, nhưng nó chưa hoàn toàn đủ; trong phương trình ban đầu, x = 1 là một nghiệm, nhưng x = –27 cũng là một nghiệm.
Suốt hàng ngàn năm, các nhà toán học đã bỏ qua các nghiệm âm của phương trình vì họ chỉ làm việc với những đại lượng như chiều dài, diện tích và thể tích—những khái niệm không thể là số âm. Ý nghĩ về một hình vuông có cạnh bằng –27 là điều không thể chấp nhận được. Vì vậy, các số âm không được công nhận; người ta có thể trừ các số dương để tìm hiệu, nhưng không thể có được một kết quả âm hoặc hệ số âm. Thực tế, thay vì có một công thức bậc hai duy nhất, có tới sáu phiên bản khác nhau được sắp xếp sao cho tất cả các hệ số đều dương.
Cách tiếp cận tương tự cũng được áp dụng cho các phương trình bậc ba. Vào thế kỷ 11, nhà toán học Ba Tư Omar Khayyam đã phân loại ra 19 dạng phương trình bậc ba khác nhau, một lần nữa giữ cho tất cả các hệ số đều dương. Ông tìm ra các nghiệm số cho một số dạng phương trình bằng cách xét giao điểm của các hình học như hyperbola và đường tròn, nhưng ông không đạt được mục tiêu cuối cùng là tìm ra nghiệm tổng quát cho phương trình bậc ba. Ông đã viết: “Có lẽ một trong số những người sau chúng ta sẽ thành công trong việc tìm ra nó.”

400 năm sau và cách xa 4.000 km, giải pháp bắt đầu hiện ra. Scipione del Ferro, một giáo sư toán tại Đại học Bologna, đã phát hiện vào khoảng năm 1510 một phương pháp giải các phương trình bậc ba “trong” (các phương trình không có hạng x²). Sau khi giải được bài toán mà hàng ngàn năm trước các nhà toán học đều không thể vượt qua—một vấn đề được cho là không thể giải bởi thầy dạy toán của Leonardo da Vinci—del Ferro đã chọn giữ bí mật giải pháp của mình. Là một nhà toán học sống vào thế kỷ 16, công việc của bạn luôn bị đe dọa bởi những đối thủ có thể thách đấu bạn trong một “cuộc đối đầu toán học.” Trong các cuộc đối đầu như vậy, mỗi người sẽ được giao một bộ đề bài và người giải được nhiều bài hơn sẽ được giữ chức, trong khi người thua sẽ phải chịu sự nhục nhã trước công chúng. Theo del Ferro, không có ai trên thế giới nào có thể giải được phương trình bậc ba “trong” ngoài chính ông, nên bằng cách giữ bí mật giải pháp, ông đã bảo vệ được công việc của mình. Suốt gần hai thập kỷ, del Ferro giữ kín bí mật đó và chỉ tiết lộ cho học trò của mình, Antonio Fior, trên giường bệnh vào năm 1526.
Mặc dù Fior không có tài năng vượt trội như thầy dạy của mình, nhưng cậu trẻ lại đầy tham vọng. Sau cái chết của del Ferro, Fior khoe khoang về khả năng toán học của mình, đặc biệt là khả năng giải được phương trình bậc ba “trong.” Vào ngày 12 tháng 2 năm 1535, Fior thách đấu nhà toán học Niccolo Fontana Tartaglia, người mới chuyển đến quê hương của Fior ở Venice. Tartaglia, người đã trải qua nhiều nghịch cảnh từ nhỏ (mặt cậu bị một người lính Pháp cắt, để lại một vết nói lắp, do đó được mệnh danh “Tartaglia” nghĩa là “kẻ nói lắp”), phần lớn tự học và dần dần vươn lên trong xã hội Ý trở thành một nhà toán học được kính trọng.
Trong cuộc thách đấu có tính quyết định này, Tartaglia giao cho Fior 30 bài toán về phương trình bậc ba “trong,” và Fior cũng trao cho Tartaglia 30 bài toán bậc ba “trong.” Mỗi người có 40 ngày để giải xong các bài toán đó. Fior không giải được một bài nào, trong khi Tartaglia đã giải xong tất cả 30 bài chỉ trong hai giờ. Có vẻ như sự khoe khoang của Fior đã là điểm yếu của cậu. Trước khi cuộc thách đấu bắt đầu, Tartaglia đã nghi ngờ khả năng của Fior khi cậu khẳng định đã giải được phương trình bậc ba “trong,” và Tartaglia viết rằng “Tôi không cho rằng cậu có khả năng tự tìm ra một quy tắc như vậy.” Tin đồn cho rằng một nhà toán học vĩ đại đã tiết lộ bí mật cho Fior, điều này càng thúc đẩy Tartaglia tự mình tìm ra lời giải cho phương trình bậc ba “trong” để bảo vệ nghề nghiệp của mình.
Để làm được điều đó, Tartaglia đã mở rộng ý tưởng “hoàn thiện hình vuông” sang ba chiều. Hãy xét phương trình
x³ + 9x = 26.
Ở đây, x³ có thể được hiểu như thể tích của một khối lập phương có cạnh dài x. Hạng 9x biểu thị thêm một thể tích, và tổng chúng bằng 26. Giống như trong phương pháp hoàn thiện hình vuông, ta cần “thêm vào” khối lập phương để tăng thể tích thêm 9x. Hãy tưởng tượng kéo dài ba mặt của khối lập phương ra ngoài một khoảng cách y để tạo thành một khối lớn hơn với cạnh mới là z, trong đó z = x + y. Thể tích bổ sung có thể được chia thành bảy phần: ba khối hộp chữ nhật kích thước x × x × y, ba khối hộp chữ nhật hẹp kích thước x × y × y, và một khối lập phương nhỏ có thể tích bằng y³. Tartaglia sắp xếp lại sáu khối hộp thành một khối đơn với một cạnh dài 3y, cạnh kia dài (x + y) – tức là z – và chiều cao x. Thể tích của khối này bằng (3y·z) nhân với x, và Tartaglia nhận ra rằng nếu đáy (3yz) bằng 9 thì nó sẽ biểu diễn chính xác hạng 9x trong phương trình ban đầu. Ông đặt 3yz = 9. Sau khi lắp ráp lại khối, ông nhận thấy thiếu đi khối nhỏ có thể tích y³, vì vậy ông cộng y³ vào cả hai vế của phương trình. Kết quả là khối lập phương hoàn chỉnh có thể tích z³ bằng 26 + y³. Với hai phương trình và hai ẩn, ông giải phương trình đầu tiên cho z và thay vào phương trình thứ hai, thu được một phương trình chứa y⁶ và y³. Ban đầu, có vẻ như vấn đề trở nên phức tạp hơn, nhưng nếu ta coi y³ như một biến mới thì phương trình trở thành một phương trình bậc hai—loại mà ta có thể giải bằng cách hoàn thiện hình vuông. Kết quả cho thấy y³ = 1, do đó y = 1, và z = 3 (vì z = 3/y). Cuối cùng, vì x + y = z nên x = 2, đây chính là nghiệm của phương trình ban đầu. Với kết quả này, Tartaglia trở thành người thứ hai trong lịch sử giải được phương trình bậc ba “trong.”
Để tránh việc phải đi qua các bước giải hình học phức tạp cho mỗi phương trình bậc ba mới, Tartaglia đã tóm tắt phương pháp của mình thành một thuật toán – một tập hợp các hướng dẫn. Ông viết ra điều này không dưới dạng một chuỗi phương trình như ngày nay (ký hiệu đại số hiện đại sẽ chỉ xuất hiện sau khoảng một trăm năm), mà dưới dạng một bài thơ. Chiến thắng của Tartaglia đã biến ông trở thành một ngôi sao trong giới toán học, khi mà các nhà toán học khác ai cũng khao khát học được bí quyết của ông, đặc biệt là Gerolamo Cardano, một nhà đa học ở Milan. Tuy nhiên, Tartaglia từ chối tiết lộ bất kỳ đề bài nào từ cuộc thi. Cardano, kiên trì trong nỗ lực của mình, đã viết một loạt các bức thư xen kẽ giữa lời ca ngợi và những chỉ trích gay gắt. Cuối cùng, với lời hứa được giới thiệu đến nhà bảo trợ giàu có của mình, Cardano đã dụ được Tartaglia đến Milan. Vào ngày 25 tháng 3 năm 1539, Tartaglia đã tiết lộ phương pháp của mình, nhưng chỉ sau khi ép Cardano phải thề không được tiết lộ, không được công bố và chỉ viết nó dưới dạng mã hóa, với lời tuyên bố: “Để sau khi tôi chết, không ai có thể hiểu được nó.” Cardano vô cùng vui mừng và lập tức bắt đầu thử nghiệm thuật toán của Tartaglia. Tuy nhiên, Cardano có một mục tiêu cao cả hơn: tìm ra nghiệm của phương trình bậc ba đầy đủ, bao gồm cả hạng x². Thật kỳ diệu, Cardano phát hiện ra rằng nếu ta thay x bằng (x – b⁄(3a)) thì tất cả các hạng x² sẽ triệt tiêu lẫn nhau. Đây chính là cách để biến bất kỳ phương trình bậc ba tổng quát nào thành phương trình bậc ba “trong,” từ đó có thể giải bằng công thức của Tartaglia. Cardano hào hứng đến mức muốn công bố phát hiện của mình, giải quyết được bài toán đã làm bế tắc những nhà toán học giỏi nhất suốt hàng nghìn năm. Khác với các đồng nghiệp, Cardano không cảm thấy cần phải giữ kín giải pháp; ông kiếm sống không chỉ bằng toán học mà còn bằng nghề y và danh tiếng của mình, và với ông, danh dự còn quý giá hơn bí mật. Vấn đề duy nhất là lời thề ông đã thề với Tartaglia, khiến ông không thể tiết lộ.
Có thể bạn nghĩ rằng đó sẽ là kết thúc của câu chuyện, nhưng vào năm 1542, Cardano đã đến Bologna và gặp một nhà toán học, người tình cờ là con rể của Scipione del Ferro – người đã, trên giường bệnh, truyền lại lời giải của phương trình bậc ba “trong” cho Antonio Fior. Trong chuyến thăm đó, Cardano được cho xem cuốn sổ tay cũ của del Ferro chứa đựng một lời giải có thời gian xuất hiện sớm hơn lời giải của Tartaglia hàng thập kỷ. Như vậy, theo Cardano, ông có thể công bố nghiệm đầy đủ của phương trình bậc ba mà không vi phạm lời thề với Tartaglia. Ba năm sau, Cardano xuất bản cuốn Ars Magna (Nghệ Thuật Vĩ Đại), một tập hợp cập nhật về toán học, với dòng chữ “Viết trong năm năm, mong nó kéo dài năm trăm năm.” Trong Ars Magna, Cardano đã viết một chương trình chứng minh hình học độc đáo cho mỗi trong 13 cách sắp xếp của phương trình bậc ba. Mặc dù ông ghi nhận những đóng góp của Tartaglia, del Ferro và Fior, nhưng Tartaglia lại vô cùng không hài lòng. Ông đã gửi những bức thư xúc phạm cho Cardano và gửi bản sao cho một phần lớn cộng đồng toán học. Đến nay, nghiệm tổng quát của phương trình bậc ba vẫn thường được gọi là “phương pháp của Cardano,” dù Ars Magna vẫn là một thành tựu phi thường, đẩy lý luận hình học đến giới hạn của nó—thực sự đến mức “vỡ óc.”
Trong quá trình viết Ars Magna, Cardano gặp phải những phương trình bậc ba mà không thể giải theo cách thông thường, chẳng hạn như
x³ = 15x + 4.
Khi áp dụng thuật toán, lời giải thu được chứa căn bậc hai của số âm. Cardano hỏi Tartaglia về trường hợp này, nhưng Tartaglia né tránh và ám chỉ rằng Cardano không đủ thông minh để sử dụng công thức của ông một cách đúng đắn. Thực tế là Tartaglia cũng không biết phải làm gì trong trường hợp này. Cardano đã quay trở lại phân tích dẫn chứng hình học của một bài toán tương tự để tìm hiểu chính xác lỗi phát sinh ở đâu. Mặc dù phương pháp “cắt khối lập phương ba chiều và sắp xếp lại” hoạt động tốt, bước cuối cùng—hoàn thiện hình vuông của phương trình bậc hai—lại dẫn đến một nghịch lý hình học. Cardano nhận thấy một phần của hình vuông cần có diện tích 30 nhưng các cạnh của nó lại chỉ dài 5, trong khi một hình vuông đầy đủ với cạnh 5 chỉ có diện tích 25. Để “hoàn thiện” hình vuông, Cardano buộc phải cộng thêm một diện tích “âm.” Chính đó đã là nguồn gốc của căn bậc hai của số âm, ý tưởng về diện tích âm.
Đây không phải là lần đầu tiên căn bậc hai của số âm xuất hiện trong toán học. Thực tế, trước đó trong Ars Magna cũng đã có bài toán “Tìm hai số có tổng bằng 10 và tích bằng 40.” Khi gộp các điều kiện này thành một phương trình bậc hai:
x² – 10x + 40 = 0,
áp dụng công thức bậc hai cho ta sẽ có nghiệm chứa căn bậc hai của số âm. Kết luận hiển nhiên là không có nghiệm thực nào, vì không tồn tại hai số thực nào có tổng bằng 10 và tích bằng 40. Các nhà toán học đã hiểu rằng căn bậc hai của số âm là dấu hiệu cho biết không có nghiệm trong tập hợp số thực. Tuy nhiên, với phương trình bậc ba này, qua vài lần thử và sai, ta có thể tìm ra x = 4 là một nghiệm hợp lý. Vậy tại sao cách giải thông thường không tìm ra nghiệm này? Không thể nhìn thấy một lối đi rõ ràng, Cardano đã chọn cách bỏ qua trường hợp này trong Ars Magna, nói rằng khái niệm căn bậc hai của số âm “tinh vi nhưng vô dụng.” Nhưng khoảng 10 năm sau, kỹ sư người Ý Rafael Bombelli đã tiếp tục công việc của Cardano. Không nản lòng trước căn bậc hai của số âm và nghịch lý hình học mà nó gợi ra, Bombelli quyết tâm tìm ra lối giải cho vấn đề này. Ông nhận thấy rằng căn bậc hai của số âm “không thể gọi là dương hay âm” và do đó nên được coi là một loại số mới. Bombelli cho rằng hai số hạng trong lời giải của Cardano có thể được biểu diễn như là sự kết hợp của một số thực và loại số mới này (với căn bậc hai của –1). Theo cách đó, Bombelli chứng minh rằng hai căn bậc ba trong công thức của Cardano tương đương với “hai ± căn bậc hai của –1.” Khi thực hiện bước cuối cùng và cộng chúng lại, các căn bậc hai triệt tiêu lẫn nhau, để lại kết quả chính xác là 4. Điều này dường như thật kỳ diệu. Phương pháp của Cardano thực sự hiệu quả, nhưng ta buộc phải từ bỏ cách chứng minh hình học ban đầu—các diện tích âm, mặc dù không có ý nghĩa trong thực tế, lại phải được chấp nhận như một bước trung gian để dẫn đến lời giải đúng.
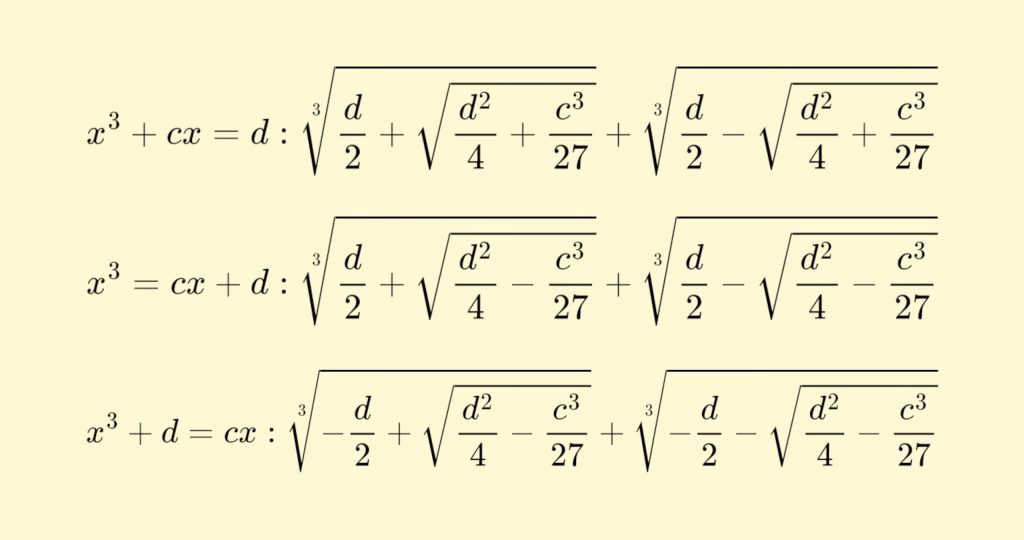
Trong vòng một trăm năm sau đó, toán học hiện đại bắt đầu hình thành. Vào thế kỷ 17, François Viète đã giới thiệu ký hiệu đại số hiện đại, chấm dứt truyền thống hàng ngàn năm khi các bài toán được diễn đạt qua hình vẽ và mô tả bằng lời. Hình học không còn là nguồn chân lý tối thượng. René Descartes sử dụng nhiều căn bậc hai của số âm, từ đó làm quen với chúng; dù ông nhận ra tính hữu ích của chúng, ông lại gọi chúng là “số ảo” – một cái tên đã tồn tại cho đến nay. Sau đó, Euler giới thiệu chữ “i” để biểu thị căn bậc hai của –1. Khi kết hợp với các số thực, chúng tạo thành tập hợp số phức. Việc giải phương trình bậc ba đã dẫn đến phát minh ra những con số mới này và giải phóng đại số khỏi sự ràng buộc của hình học. Bằng cách từ bỏ những mô tả trực quan của hiện thực, ta có được một toán học mạnh mẽ và hoàn chỉnh hơn để giải quyết các bài toán thực tế, và hóa ra phương trình bậc ba chỉ là khởi đầu.
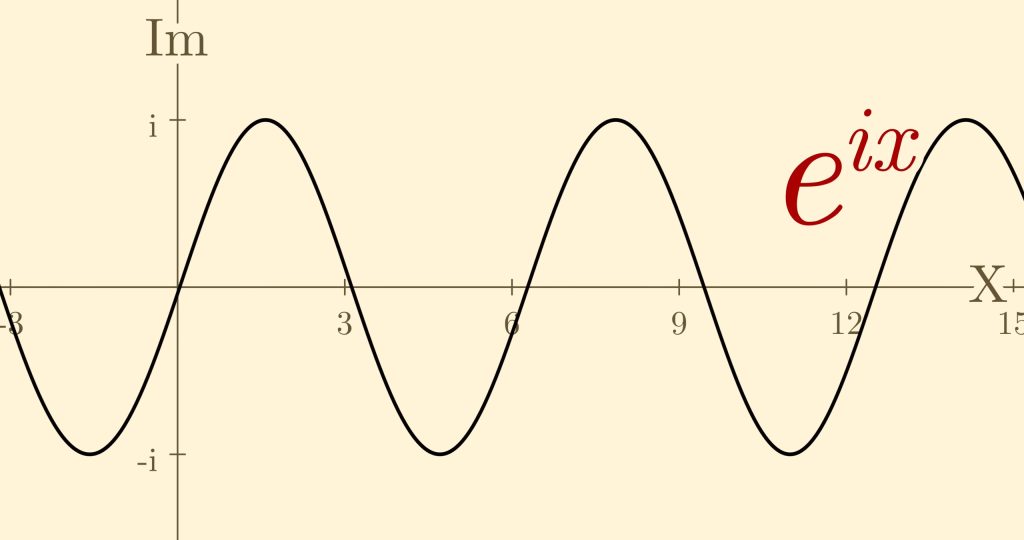
Năm 1925, Erwin Schrödinger tìm kiếm một phương trình sóng để mô tả hành vi của các hạt lượng tử, dựa trên nhận định của de Broglie rằng vật chất có tính chất sóng. Ông đã đưa ra một trong những phương trình quan trọng và nổi tiếng nhất trong vật lý học, đó là phương trình Schrödinger, trong đó số i (căn bậc hai của –1) đóng vai trò then chốt. Mặc dù các nhà toán học đã quen với số ảo, nhiều nhà vật lý vẫn cảm thấy không thoải mái khi chúng xuất hiện trong một lý thuyết nền tảng như vậy. Chính Schrödinger đã viết: “Điều không dễ chịu ở đây, và thực sự cần bị phản đối, là việc sử dụng số phức. Hàm sóng Ψ chắc chắn về bản chất là một hàm số thực.” Lời phản đối này nghe có vẻ hợp lý, vậy tại sao một số ảo, vốn xuất hiện lần đầu tiên trong lời giải phương trình bậc ba, lại xuất hiện trong vật lý nền tảng? Lý do nằm ở những tính chất độc đáo của số ảo. Số ảo tồn tại trên một chiều vuông góc với trục số thực, và khi kết hợp với các số thực, chúng tạo thành mặt phẳng phức. Ví dụ, khi nhân liên tục với i, bắt đầu từ 1: 1 × i = i, i × i = –1 (theo định nghĩa), –1 × i = –i, và –i × i = 1, ta thấy mỗi lần nhân, kết quả quay 90° và quá trình này lặp đi lặp lại. Thực tế, khi bạn nhân với i, bạn đang quay số đó 90° trên mặt phẳng phức.
Có một hàm số mà khi di chuyển dọc theo trục x liên tục nhân với i, đó chính là e^(i·x). Hàm số này tạo ra một đường xoáy, như thể các góc quay được trải đều dọc theo trục x. Phần thực của đường xoáy này là một sóng cosine, còn phần ảo là một sóng sine; đây là hai hàm cơ bản mô tả sóng. Khi Schrödinger xây dựng phương trình sóng của mình, ông tự nhiên giả định rằng các nghiệm của phương trình sẽ có dạng e^(i·kx – ωt). Bạn có thể thắc mắc tại sao ông lại sử dụng dạng hàm mũ này thay vì chỉ dùng một sóng sine đơn giản. Câu trả lời là hàm mũ có những tính chất hữu ích: đạo hàm của nó theo vị trí hoặc thời gian tỉ lệ với chính nó—điều mà hàm sine không có (vì đạo hàm của sine là cosine). Hơn nữa, vì phương trình Schrödinger là tuyến tính, nên ta có thể cộng lại vô số nghiệm có dạng như vậy để tạo ra bất kỳ hình dạng sóng nào, và tổng đó cũng sẽ là một nghiệm của phương trình.
Nhà vật lý Freeman Dyson sau này đã viết: “Schrödinger đưa căn bậc hai của –1 vào phương trình, và đột nhiên mọi thứ trở nên hợp lý. Đột nhiên nó trở thành một phương trình sóng thay vì một phương trình dẫn nhiệt. Và Schrödinger vui mừng phát hiện ra rằng phương trình có những nghiệm tương ứng với các quỹ đạo lượng tử trong mô hình Bohr của nguyên tử. Hóa ra, phương trình Schrödinger mô tả chính xác mọi thứ chúng ta biết về hành vi của các nguyên tử. Nó là nền tảng của toàn bộ hóa học và phần lớn vật lý học. Và căn bậc hai của –1 có nghĩa là tự nhiên vận hành với số phức chứ không phải với số thực. Phát hiện này đến như một bất ngờ hoàn toàn, đối với cả Schrödinger lẫn mọi người.”
Vậy, số ảo – ban đầu được phát hiện như một bước trung gian “kỳ quặc” trong việc giải phương trình bậc ba – lại trở thành yếu tố nền tảng trong mô tả hiện thực của chúng ta. Chỉ khi từ bỏ mối liên hệ trực tiếp của toán học với hình học có thể chạm vào thực tại, ta mới có thể hướng tới một chân lý sâu xa hơn về cách thức hoạt động của vũ trụ.




