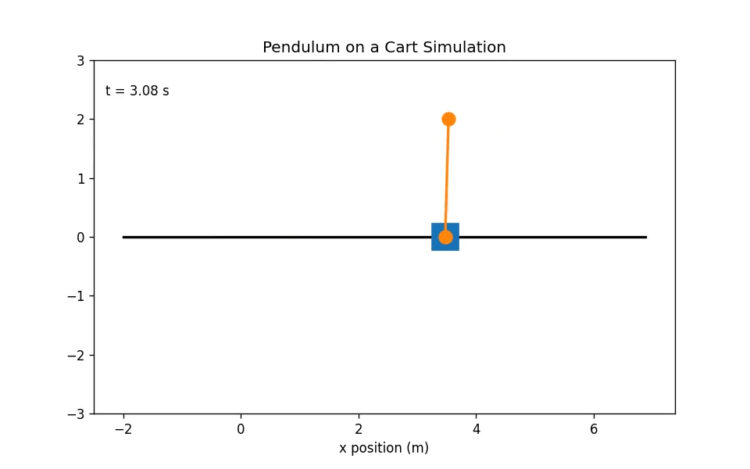
Trong bài viết này, chúng ta sẽ tìm hiểu cách các mô hình tạo lập thị trường hoạt động về mặt toán học và cách bạn có thể thiết kế mô hình tạo lập thị trường của riêng mình!
Trước khi đi sâu vào việc tạo lập thị trường, trước tiên chúng ta sẽ tìm hiểu về toán học đằng sau một ý tưởng tổng quát hơn… cân bằng một con lắc lộn ngược.
Con lắc trên xe đẩy
Hãy xem bức vẽ tuyệt đẹp của tôi về một con lắc gắn vào ô tô:
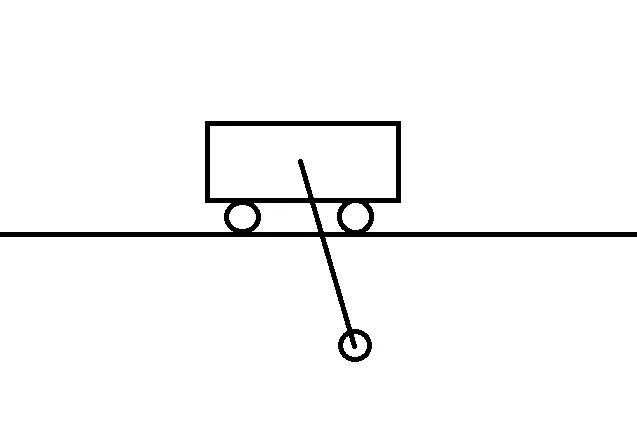
Chúng ta có thể tác dụng một lực (u) lên xe (lực dương để di chuyển sang phải và lực âm để di chuyển sang trái). Liệu chúng ta có thể giữ thăng bằng con lắc ở đỉnh chỉ bằng cách làm như vậy không?
Có chứ! Hồi nhỏ bạn đã từng giữ thăng bằng một cây chổi trên tay chưa? Nguyên lý cũng tương tự.
Tuyệt vời, nhưng chúng ta phải làm thế nào đây?
Trước tiên, chúng ta cần tìm hiểu động lực học của hệ thống. Giả sử chúng ta có thể đo lường một vài thông số:
- x: Vị trí của xe
- x’: Tốc độ của xe
- theta: Góc của con lắc
- theta’: Tốc độ thay đổi của góc.
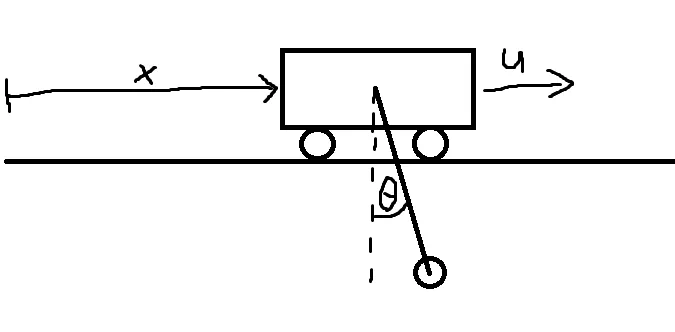
4 điều đó tạo nên “trạng thái” của hệ thống chúng ta.
Tôi sẽ không làm bạn chán với cách suy luận hệ vật lý ở đây đâu, tôi không phải nhà vật lý. Cứ tin tôi đi, hệ vật lý ở đây là:
Có rất nhiều biểu tượng ở đây… chúng ta hãy cùng tìm hiểu ý nghĩa của chúng:
- L: Chiều dài của con lắc
- M: Khối lượng của xe
- m: Khối lượng của con lắc
- g: Hằng số hấp dẫn
- delta: Mô-men xoắn giảm chấn
Chúng ta hãy mô phỏng điều này chỉ với một lực không đổi:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import matplotlib.animation as animation
from scipy.integrate import solve_ivp
from scipy.linalg import solve_continuous_are
duration=10
fps = 60
# Parameters
M = 2.0 # cart mass
m = 1 # pendulum mass
L = 2.0 # pendulum length
delta = 0.001 # Pendulum drag
g = 9.81
theta0 = np.pi - 0.75
theta_dot0 = 0
x0 = 0
x_dot0 = 0
# Control input (force on cart)
def u():
return 0.5
# ODE system
def dynamics(t, y):
x, x_dot, theta, theta_dot = y
# --- with viscous pivot damping c = delta ---
denom = (M + m*np.sin(theta)**2)
theta_ddot = -(
(L**2 * m**2 * theta_dot**2 * np.sin(2*theta))
+ 2*L*g*m*(M+m)*np.sin(theta)
+ 2*L*m*u()*np.cos(theta)
+ 2*delta*(M+m)*theta_dot
) / (2 * L**2 * m * denom)
x_ddot = (
(L**2 * m * theta_dot**2 * np.sin(theta))
+ 0.5*L*g*m*np.sin(2*theta)
+ L*u()
+ delta*theta_dot*np.cos(theta)
) / (L * denom)
return [x_dot, x_ddot, theta_dot, theta_ddot]
t_eval = np.linspace(0, duration, int(duration*fps/2))
sol = solve_ivp(dynamics, [0, duration], [x0, x_dot0, theta0, theta_dot0], t_eval=t_eval)
# Extract solution
x, theta = sol.y[0], sol.y[2]
# Convert to x, y coordinates
pendulum_x = x + L * np.sin(theta)
pendulum_y = -L * np.cos(theta)
# --- Animation setup ---
fig, ax = plt.subplots(figsize=(8, 5))
ax.set_xlim(np.min(x) - L - 0.5, np.max(x) + L + 0.5)
ax.set_ylim(-1.5*L, 1.5*L)
ax.set_aspect(’equal’)
ax.set_xlabel(”x position (m)”)
ax.set_title(”Pendulum on a Cart Simulation”)
# Elements to animate
track, = ax.plot([], [], ‘k-’, lw=2)
cart, = ax.plot([], [], ‘s’, color=’tab:blue’, markersize=20)
rod, = ax.plot([], [], ‘o-’, color=’tab:orange’, lw=2, markersize=10)
time_text = ax.text(0.02, 0.9, ‘’, transform=ax.transAxes)
# --- Initialization ---
def init():
track.set_data([], [])
cart.set_data([], [])
rod.set_data([], [])
time_text.set_text(’‘)
return track, cart, rod, time_text
# --- Animation update function ---
def update(i):
cart_x = x[i]
cart_y = 0.0
# Pendulum line endpoints
rod_x = [cart_x, pendulum_x[i]]
rod_y = [cart_y, pendulum_y[i]]
# Track line
track.set_data([np.min(x) - L, np.max(x) + L], [0, 0])
cart.set_data([cart_x], [cart_y])
rod.set_data(rod_x, rod_y)
time_text.set_text(f”t = {sol.t[i]:.2f} s”)
return track, cart, rod, time_text
# --- Create animation ---
ani = FuncAnimation(
fig, update, frames=len(t_eval),
init_func=init, interval=1/fps, blit=True
)
import imageio_ffmpeg, matplotlib
matplotlib.rcParams[’animation.ffmpeg_path’] = imageio_ffmpeg.get_ffmpeg_exe()
writer = animation.FFMpegWriter(fps=fps, bitrate=9000) # ~9 Mbps
ani.save(”inverted_pendulum.mp4”, writer=writer, dpi=120)
plt.show()Trước khi tiếp tục với ví dụ về con lắc, trước tiên chúng ta cần hiểu một số lý thuyết.
Hệ thống ODE tuyến tính
Hãy xem xét hệ phương trình vi phân tuyến tính sau:
Giải pháp cho vấn đề này được đưa ra bởi
e mũ ma trận ư? Cái quái gì thế này? Thực ra, khá đơn giản nếu chúng ta xét chuỗi Taylor của hàm mũ:
Đừng lo lắng, thực ra bạn không cần phải đánh giá điều này.
Thay vào đó, chúng ta có thể làm một điều thực sự thú vị gọi là đường chéo hóa, trong đó chúng ta viết lại A như sau:
Trong đó D là ma trận đường chéo được tạo thành từ các giá trị riêng của A, và T là ma trận được tạo thành từ các vectơ riêng của A. Để biết thêm chi tiết về thời điểm chính xác một ma trận có thể và không thể chéo hóa, hãy xem trang Wikipedia: https://en.wikipedia.org/wiki/Diagonalizable_matrix
Theo nguyên tắc chung, hầu hết các ma trận chuẩn mà bạn sử dụng có thể đều có thể chéo hóa được.
Điều gì sẽ xảy ra nếu bây giờ chúng ta lấy A lũy thừa 2?
Ồ, hay quá, lũy thừa đã được chuyển vào ma trận đường chéo.
Thực tế, với bất kỳ n nào, ta có:
Đưa điều này vào định nghĩa của e^{At}, chúng ta cũng dễ dàng thấy rằng:
Tuyệt vời… vậy là thay vì phải tính e^{At}, giờ chúng ta phải chéo hóa A và VẪN tính ma trận mũ e^{Dt}. Mục đích là gì?
Vấn đề là việc tính toán hàm mũ của ma trận đường chéo cực kỳ dễ dàng.
Lời giải là:
Trong đó lambda_i*t là phần tử đường chéo thứ i của Dt, và các lambda đó là các giá trị riêng của A. Vì vậy, chúng ta chỉ cần chéo hóa và sau đó lấy số mũ của SCALARS, điều này cực kỳ dễ dàng.
Đưa điều này trở lại giải pháp của hệ phương trình vi phân tuyến tính của chúng ta:
Chúng ta có thể nói gì về tính ổn định của nghiệm này? Nó có tăng đến vô cực không? Nó có hội tụ về 0 không? Nó có dao động không? Nghiệm nằm trong ma trận e^{Dt}! của chúng ta.
Giá trị riêng là số phức:
Từ phân tích phức tạp, chúng ta có mỗi phần tử đường chéo của e^{Dt} có dạng:
Phần bên trong ngoặc luôn có biên độ là 1, nên ta không cần phải lo lắng về nó. Tuy nhiên, e^{at} sẽ tăng vọt khi a > 0 và hội tụ về 0 khi a < 0.
a là phần thực của giá trị riêng của chúng ta, do đó chúng ta đi đến kết luận cuối cùng:
Giải pháp của hệ thống chúng ta là ổn định và hội tụ về 0 nếu phần thực của các giá trị riêng của A là âm!
Tuyến tính hóa quanh một điểm cố định
Bây giờ, giả sử chúng ta có một hệ thống phi tuyến tính:
Mục tiêu của chúng tôi là tuyến tính hóa hệ thống này và thu được giải pháp gần đúng:
mà chúng ta đã biết lý thuyết.
Bước đầu tiên là tìm các số không của f:
Theo định lý Taylor, ta có:
Nếu chúng ta bỏ qua mọi thứ sau số hạng bậc nhất, chúng ta sẽ có phép tính gần đúng tuyến tính:
Lưu ý rằng f(\bar{x}) bằng 0! Đây là lý do tại sao chúng ta cần f bằng 0.
Thứ Df/Dx này được gọi là Jacobian của f:
và chúng ta đánh giá nó ở giá trị không \bar{x}.
Vì vậy, nếu chúng ta định nghĩa y = x – \bar{x} thì chúng ta có:
Vì vậy, bằng cách định nghĩa A là ma trận Jacobian được đánh giá tại \bar{x}, cuối cùng chúng ta có:
Và bạn đã biết cách giải y và xem nó có ổn định hay không. Sau đó, bạn chỉ cần thêm \bar{x} vào y để có được nghiệm gần đúng x!
Khả năng kiểm soát
Quay lại ví dụ về con lắc ô tô của chúng ta. Chúng ta có:
Các số không của f này được đưa ra bởi:
- x: tùy ý (không hiển thị ở đâu cả)
- x_dot: 0 (để làm cho hàng đầu tiên là 0)
- theta: k*pi (Tương ứng với tăng hoặc giảm. K lẻ là tăng và k chẵn là giảm).
- theta_dot: 0 (để làm cho hàng thứ ba bằng 0)
Chúng ta muốn cân bằng xe ở vị trí thẳng đứng, vì vậy tôi sẽ chọn x=3, x_dot=0, theta=pi, theta_dot=0.
Jacobian của f được đánh giá tại số không cụ thể này là:
Vì vậy, chúng ta thu được:
Giờ đến phần thú vị! Mặc dù chúng ta không thể kiểm soát trực tiếp vị trí của xe hoặc góc, chúng ta CÓ THỂ kiểm soát lực u tác dụng lên xe, và lực này xuất hiện trong hàm f. Nếu lấy đạo hàm của f theo u, ta sẽ có:
Và cuối cùng chúng ta thu được:
Lưu ý: Trong trường hợp của chúng ta, u chỉ là một biến duy nhất, nhưng trên thực tế, bạn có thể kiểm soát nhiều thứ (giống như chúng ta đang tạo lập thị trường, chúng ta sẽ tìm hiểu sau!).
Lưu ý khác: Cũng có thể bạn không thể đo trực tiếp trạng thái của mình mà thay vào đó là một số y = Cx khác, nhưng hiện tại chúng ta giả sử rằng chúng ta *có thể* đo các trạng thái sao cho y = x.
Mục tiêu của chúng ta bây giờ là tìm một ma trận K sao cho u = -Kx điều khiển hệ thống theo một cách “tối ưu” nào đó và hướng nó đến sự ổn định. “Tối ưu” có thể mang nhiều nghĩa khác nhau; chúng ta sẽ thảo luận về một ví dụ sau.
Nếu chúng ta viết lại hệ thống của mình với u = -Kx, chúng ta sẽ có:
Và như chúng ta đã biết từ lý thuyết về hệ phương trình vi phân tuyến tính, để nghiệm của phương trình này ổn định, ta cần phần thực của các giá trị riêng của (A-BK) phải âm. Ta có thể chọn K để kiểm soát tính ổn định của nghiệm bằng cách chọn một K tốt.
Lưu ý: Chúng ta không nhất thiết có thể điều khiển hệ thống bằng biến điều khiển u. Giả sử biến điều khiển u là số lượng bánh taco chúng ta ăn vào thứ Năm. Tôi không nghĩ chúng ta có thể điều khiển ô tô hay con lắc bằng biến đó… Để tìm hiểu thêm về tính điều khiển, hãy đọc bài viết sau trên Wikipedia: https://en.wikipedia.org/wiki/Controllability .
Chúng ta sẽ giả định rằng hệ thống của chúng ta có thể điều khiển được từ bây giờ.
Nếu một hệ thống có thể điều khiển được, chúng ta có thể đạt được bất kỳ giá trị riêng tùy ý nào của (A-BK) bằng cách chọn K một cách thông minh.
Bộ điều chỉnh tuyến tính bậc hai
Được rồi, vậy thì các phần thực của các giá trị riêng của (A-BK) cần phải âm… Tại sao không làm cho chúng siêu âm, và sau đó hệ thống của chúng ta sẽ hội tụ thực sự, thực sự nhanh chóng!
Không nhanh như vậy đâu.
Có 2 vấn đề chính với cách tiếp cận này:
- Sự kiểm soát của chúng ta đến từ phép xấp xỉ tuyến tính của hệ thống. Nếu bạn di chuyển quá mức, phép xấp xỉ tuyến tính sẽ trở nên không chính xác, và bạn thực sự có thể đi chệch hướng.
- Việc kiểm soát có thể liên quan đến một số chi phí. Trong trường hợp con lắc của chúng ta, khi chúng ta tác dụng một lực nào đó lên xe, thì đây có thể là lượng xăng chúng ta tiêu thụ.
Vì vậy, chúng ta muốn chọn các giá trị riêng giúp hệ thống của chúng ta hướng tới sự ổn định theo cách tốt đẹp và trơn tru.
Để làm được điều này, chúng ta có thể định nghĩa hàm chi phí sau:
trong đó Q và R là các ma trận bán xác định dương.
Nếu chúng ta không đạt được mục tiêu một cách nhanh chóng thì phần Q sẽ rất lớn và nếu phần u của chúng ta thực sự lớn và chúng ta tiêu tốn rất nhiều năng lượng thì phần R của chúng ta sẽ rất lớn.
Vậy Q và R cho phép chúng ta kiểm soát tầm quan trọng của sự hội tụ nhanh và hiệu quả năng lượng đối với chúng ta.
Trong trường hợp này, tôi sẽ chọn:
Tin tốt đây: Thực sự có một ma trận K tối thiểu hóa hàm chi phí J!
Tin xấu: Phần toán học phức tạp hơn và đòi hỏi phải giải một phương trình Riccati đại số. Chúng ta sẽ để thư viện xử lý việc này. Nếu bạn muốn tìm hiểu thêm về toán học đằng sau điều này, hãy tra cứu các thuật ngữ “Phương trình Riccati Đại số” và “Phương trình Hamilton-Jacobi Bellman”.
Chúng ta thu được:
trong đó P là nghiệm của phương trình riccati đại số:
Và giờ thì chúng ta đã hoàn thành! Bài tập K này sẽ giúp chúng ta tác dụng lực lên xe theo một cách rất cụ thể, giúp ổn định hệ thống và cân bằng con lắc một cách mượt mà!
Sau đây là toàn bộ nội dung được mã hóa:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import matplotlib.animation as animation
from scipy.integrate import solve_ivp
from scipy.linalg import solve_continuous_are
duration=10
fps = 60
# Parameters
M = 2.0 # cart mass
m = 1 # pendulum mass
L = 2.0 # pendulum length
delta = 0.001 # Pendulum drag
g = 9.81
theta0 = np.pi - 0.75
theta_dot0 = 0
x0 = 0
x_dot0 = 0
A = np.array([[0, 1, 0, 0],
[0, 0, g*m/M, -delta/(L*M)],
[0, 0, 0, 1],
[0, 0, g*(M+m)/(L*M), -delta*(M+m)/(L*L*M*m)]])
B = np.array([[0],[1/M],[0],[1/(L*M)]])
Q = np.array([[1,0,0,0],
[0,1,0,0],
[0,0,10,0],
[0,0,0,1]])
R = 0.01*np.eye(1)
P = solve_continuous_are(A, B, Q, R)
K = np.linalg.inv(R) @ B.T @ P
# Control input (force on cart)
def u(y):
y_hat = [y[0]-3, y[1], y[2]-np.pi, y[3]]
u_val = -K@y_hat
return u_val[0]
# ODE system
def dynamics(t, y):
x, x_dot, theta, theta_dot = y
# --- with viscous pivot damping c = delta ---
denom = (M + m*np.sin(theta)**2)
theta_ddot = -(
(L**2 * m**2 * theta_dot**2 * np.sin(2*theta))
+ 2*L*g*m*(M+m)*np.sin(theta)
+ 2*L*m*u(y)*np.cos(theta)
+ 2*delta*(M+m)*theta_dot
) / (2 * L**2 * m * denom)
x_ddot = (
(L**2 * m * theta_dot**2 * np.sin(theta))
+ 0.5*L*g*m*np.sin(2*theta)
+ L*u(y)
+ delta*theta_dot*np.cos(theta)
) / (L * denom)
return [x_dot, x_ddot, theta_dot, theta_ddot]
t_eval = np.linspace(0, duration, int(duration*fps/2))
sol = solve_ivp(dynamics, [0, duration], [x0, x_dot0, theta0, theta_dot0], t_eval=t_eval)
# Extract solution
x, theta = sol.y[0], sol.y[2]
# Convert to x, y coordinates
pendulum_x = x + L * np.sin(theta)
pendulum_y = -L * np.cos(theta)
# --- Animation setup ---
fig, ax = plt.subplots(figsize=(8, 5))
ax.set_xlim(np.min(x) - L - 0.5, np.max(x) + L + 0.5)
ax.set_ylim(-1.5*L, 1.5*L)
ax.set_aspect(’equal’)
ax.set_xlabel(”x position (m)”)
ax.set_title(”Pendulum on a Cart Simulation”)
# Elements to animate
track, = ax.plot([], [], ‘k-’, lw=2)
cart, = ax.plot([], [], ‘s’, color=’tab:blue’, markersize=20)
rod, = ax.plot([], [], ‘o-’, color=’tab:orange’, lw=2, markersize=10)
time_text = ax.text(0.02, 0.9, ‘’, transform=ax.transAxes)
# --- Initialization ---
def init():
track.set_data([], [])
cart.set_data([], [])
rod.set_data([], [])
time_text.set_text(’‘)
return track, cart, rod, time_text
# --- Animation update function ---
def update(i):
cart_x = x[i]
cart_y = 0.0
# Pendulum line endpoints
rod_x = [cart_x, pendulum_x[i]]
rod_y = [cart_y, pendulum_y[i]]
# Track line
track.set_data([np.min(x) - L, np.max(x) + L], [0, 0])
# ✅ Wrap scalar values in lists
cart.set_data([cart_x], [cart_y])
rod.set_data(rod_x, rod_y)
time_text.set_text(f”t = {sol.t[i]:.2f} s”)
return track, cart, rod, time_text
# --- Create animation ---
ani = FuncAnimation(
fig, update, frames=len(t_eval),
init_func=init, interval=1/fps, blit=True
)
import imageio_ffmpeg, matplotlib
matplotlib.rcParams[’animation.ffmpeg_path’] = imageio_ffmpeg.get_ffmpeg_exe()
writer = animation.FFMpegWriter(fps=fps, bitrate=9000) # ~9 Mbps
ani.save(”inverted_pendulum.mp4”, writer=writer, dpi=120)
plt.show()Đó là rất nhiều công việc… bây giờ chúng ta hãy đến với phần mà chúng ta THỰC SỰ quan tâm…